Question

How many term of the ap -10,-8...must be taken to get the sum of 26

Answer 1

13

Explanation:

The sum to n terms of an AP is

`S_(n)` =
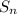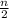`(n)/(2)` [ 2a₁ + (n - 1)d ]

where a₁ is the first term and d the common difference

Here
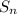`S_(n)` = 26, a₁ = - 10 and d = - 8 - (- 10) = - 8 + 10 = 2 , thus

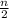`(n)/(2)` [ (2 × - 10) + 2(n - 1) ] = 26 ( multiply both sides by 2 )

n(- 20 + 2n - 2) = 52

n(- 22 + 2n) = 52

- 22n + 2n² = 52 ( subtract 52 from both sides )

2n² - 22n - 52 = 0 ( divide through by 2 )

n² - 11n - 26 = 0 ← in standard form

(n - 13)(n + 2) = 0 ← in factored form

Equate each factor to zero and solve for n

n - 13 = 0 ⇒ n = 13

n + 2 = 0 ⇒ n = - 2

However, n > 0 , thus number of terms is 13