Answer:
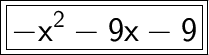
Explanation:

When there is a ( + ) in front of an expression in parentheses, there is no need to change the sign of each term in the expression. That means, the expression remains the same. Also, remove the unnecessary parentheses
⇒
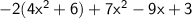
Distribute -2 through the parentheses
⇒
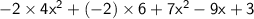
⇒
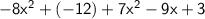
We know that ,
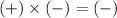
⇒
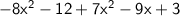
Collect like terms
⇒
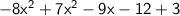
The negative and positive terms / integer are always subtracted but possess the sign of the bigger term / integer
⇒
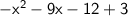
Subtract 3 from 12
⇒
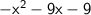
Hope I helped!
Best regards! :D