Answer:

Step-by-step explanation:
Amount of water displaced by the sphere will be equal to the volume of complete sphere.
As the sphere completely sinks to the bottom of the cup.
We have been given;
Diameter of sphere (d) = 4.6 cm
So,
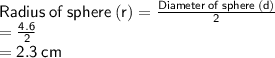
Volume of sphere (V):
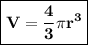
By substituting value of r we get:
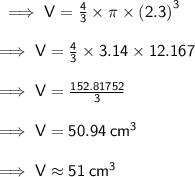
1 cm³ = 1 mL

V = 51 mL
So,
Water displaced by the sphere = 51 mL