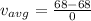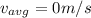Answer:
a
The winning boat is boat A
b
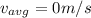
Step-by-step explanation:
From the question we are told that
The width of the lake is
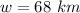
The speed of boat A to and fro is

The speed of boat B going is
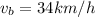
The speed of boat B coming back is
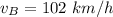
Generally the time taken by boat A is mathematically represented as
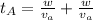
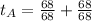
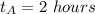
Generally the time taken by boat B is mathematically represented as
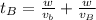
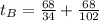
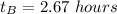
The winning boat is boat A
The average velocity is mathematically represented as
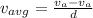
Here d is the total displacement of the winning boat which is 0 m
So