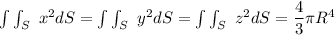Question

Let S be the sphere of radius R.

a. Argue by symmetry that

∫ ∫ x^2dS = ∫ ∫ y^2 dS= ∫ ∫ z^2dS
S S S

b. ) Use this fact and some clever thinking to evaluate, with very little computation, the integral

∫∫x^2 dS.
S

Answer 1

Explanation:

a. Given that the sphere is symmetrical in nature. If we take a look at the yz-plane, over the hemisphere, the integral on the surface of x on both sides of the plane will annul each other and the outcome will be zero. However, the remaining two integrals will also be zero as a result of symmetry on the xy and xz planes.

Thus,
`\int \int_S \ x^2 dS = \int \int_S \ y^2 dS = \int \int_S \ z^2 dS`

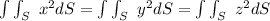
b. Recall that :

`R^2=x^2+y^2+z^2`

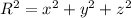
By applying the integral of the surface area.

`\int \int_S x^2 \ dS + \int \int_S y^2 \ dS + \int \int_S z^2 \ dS = R^2 \int \int_S \ dS`

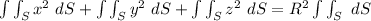
`R^2 \int \int_S \ dS = 4 \pi R^2` (surface area of a sphere)

From above;

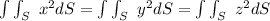
`\int \int_S \ x^2 dS = \int \int_S \ y^2 dS = \int \int_S \ z^2 dS`

∴

`\int \int_S \ x^2 dS = \int \int_S \ y^2 dS = \int \int_S \ z^2 dS = (4)/(3) \pi R^4`