Question

Please help me, I don’t understand

Answer 1

73, 74, 75

Explanation:

So the sum of three consecutive integers is 222.

Let's let the first integer be n.

Then the second integer must be (n+1).

And the third integer must be (n+2).

They total 222, thus:

`n+(n+1)+(n+2)=222`

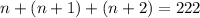
Combine like terms:

`3n+3=222`

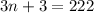
Subtract 3 from both sides:

`3n=219`

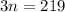
Divide both sides by 3:

`n=73`

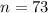
So, the first integer is 73.

So our sequence is 73, 74, and 75.

And we're done!