Answer:
Idonna's standardized score is

Jonathan's standardized score is

Jonathan had the high score
Explanation:
From the question we are told that
The score of Idonna is

The mean of SAT is

The standard deviation of SAT is

The score of Jonathan is
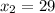
The mean of ACT is
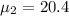
The standard deviation of ACT is

The standardized score for Idonna is
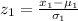
=>
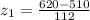
=>

The standardized score for Jonathan is
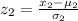
=>
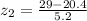
=>
