Answer:
The number of palindromes is
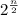 when n is even and
when n is even and
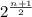 when n is odd
when n is odd
Explanation:
From the question we are told that
The length of the string is
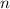
Generally palindrome is evaluated by considering the first part of a string
When the the length of the string is an even number then
it means that the first part of the string is
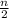
Hence the number of bit strings of length n that are palindromes is evaluated as
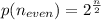
But When the the length of the string is an odd number then
it means that the first part of the string is
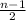
Hence the number of bit strings of length n that are palindromes is evaluated as
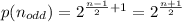
Generally each bit could be either 0 or 1
Hence the number of palindromes is
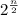 when n is even and
when n is even and
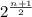 when n is odd
when n is odd