Question

The national mean sales price for a new one-family home is $181,900. A sample of 40 one-family homes in the south showed a sample mean of $166,400 and a sample standard deviation of $ 33,500.

Required:
a. Formulate the null and alternative hypothesis for this problem so the sample data support the conclusion that the population mean sales prices for new one-family homes in the South is less expensive than the national mean of $181,900.
b. What is the value of the test statistic?
c. What is the p-value?
d. At α = 0,01 what is your conclusion?

Answer 1

a

The null hypothesis is
`\mu = \$181,900`

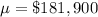
The alternative hypothesis is
`\mu < \$ 181.900`

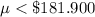
b

`t = -2.92`

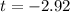
c

`p-value = 0.0016948`

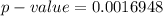
d

There no sufficient evidence to support the conclusion that the population mean sales prices for new one-family homes in the South is less expensive than the national mean of $181,900

Explanation:

From the question we are told that

The population mean is
`\mu = \$ 181, 900`

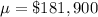
The sample size is
`n = 40`

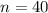
The sample mean is
`\= x = \$ 166,400`

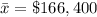
The sample standard deviation is
`s= \$ 33, 500`

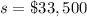
The null hypothesis is
`\mu = \$181,900`

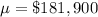
The alternative hypothesis is
`\mu < \$ 181.900`

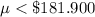
Generally the test statistics is mathematically represented as

`t = ( \= x - \mu )/( (s)/(√(n) ) )`

=>
`t = ( 166400 - 181900 )/( (33500)/(√(40) ) )`

=>
`t = -2.92`

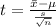
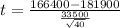
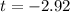
Generally the p-value is obtain from the z-table the value is

`p-value = P(Z < t ) = P(Z < -2.93) = 0.0016948`

=>
`p-value = 0.0016948`

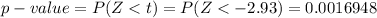
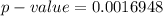
From the calculation we see that

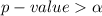`p-value > \alpha` hence we fail to reject the null hypothesis

Thus there no sufficient evidence to support the conclusion that the population mean sales prices for new one-family homes in the South is less expensive than the national mean of $181,900