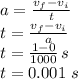Question

When jumping, a flea rapidly extends its legs, reaching a takeoff speed of 1.0 m/s over a distance of 0.50 mm. a. What is the flea's acceleration as it extends its legs? b. How long does it take the flea to leave the ground after it begins pushing off?

Answer 1

Part a) acceleration is: 1000
`(m)/(s^2)`

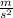
Part b) time is : 0.001 second

Step-by-step explanation:

Part a)

Notice that they don't give you information about time in the description of the take-off process, so we use the kinematic equation that relates acceleration with distance and velocity, and solve for the unknown acceleration;

`v_f^2-v_i^2= 2 * a * (x_f-x_i)`

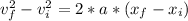
which for our case becomes:

`v_f^2-v_i^2= 2 * a * (x_f-x_i)\\(1\,(m)/(s))^2-0=2*a*(0.0005\,\,m )\\a =(1)/(0.001) \,(m)/(s^2)\\a=1000\,(m)/(s^2)`

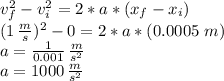
notice that we have converted the distance from mm into meters to be in agreement with the velocity units.

Part b)

we now use the definition of acceleration as the change in velocity over time to find the requested time:

`a=(v_f-v_i)/(t) \\t=(v_f-v_i)/(a)\\t=(1-0)/(1000)\, s\\t=0.001\,\,s`