Question

Let S be the sphere of radius 1 centered at (2, 4, 6). Find the distance from S to the plane x + y + z = 0.

Answer 1

5.928

Explanation:

Given that:

The relation of the plane x+y+z= 0

Suppose (x,y,z) is any point on the plane.

Then the difference between (2,4,6) to (x,y,z) is:

`d^2 = (x-2)^2 + (y -4)^2 + ( z -6)^2 \\ \\ d^2 = (x^2 -4x+4) + ( y^2-8y +16) +(z^2 -12z + 36)`

`d^2 = x^2 + y^2 +z^2 -4x -8y -12z +4 +16 +36`

`d^2 = x^2 +y^2 + z^2 -4x -8y -12z +56`

∴

`f(x,y,z) =d^2 = x^2 + y^2 + z^2 - 4x -8y - 12 z +56 - - - (1)`

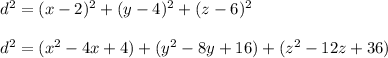
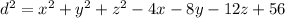
To estimate the maximum and minimum values of the function f(x,y,z) subject to the constraint g(x,y,z) = x+y+z =0

By applying Lagrane multipliers;

If we differentiate equation (1) with respect to x; we have:

f(x,y,z) = 2x -4

If we differentiate equation (1) with respect to y; we have:

f(x,y,z) = 2y - 8

If we differentiate equation (1) with respect to z; we have:

f(x,y,z) = 2z - 12

Differentiating g(x,y,z) with respect to x, we have:

`g_x(x,y,z) = 1`

Differentiating g(x,y,z) with respect to y, we have:

`g_y(x,y,z) = 1`

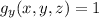
Differentiating g(x,y,z) with respect to z, we have:

`g_z(x,y,z) = 1`

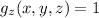
Calculating the equations
`\bigtriangledown f = \lambda \bigtriangleup g \ \ \ \& \ \ \ g(x,y,z) =0`

`f_x = \lambda g_x\\`

`2x - 4 = \lambda (1)`

`2x= 4 + \lambda`

`x= 2 + (\lambda )/(2) --- (2)`

`f_y = \lambda g_y`

`2x -8 = \lambda(1)`

`2x = 8+ \lambda`

`x = 4+(\lambda)/(2) --- (3)`

`f_z = \lambda g_z`

`2x -12 = \lambda (1)`

`x = 6 + (\lambda )/(2) --- (4)`

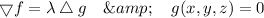
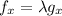
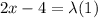
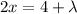
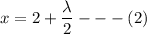
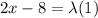
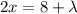
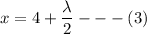
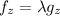
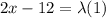
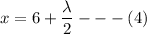
x+y+z = 0 - - - (5)

replacing x, y, z values in the given constraint

x + y + z = 0

`2+(\lambda)/(2)+4+(\lambda)/(2)+6+(\lambda)/(2)=0`

`12 + (3 \lambda )/(2)=0`

`(3 \lambda )/(2)=-12`

`3 \lambda=-12 * 2`

`3 \lambda=-24`

`\lambda=(-24)/(3)`

`\lambda=-8`

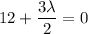
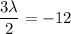
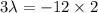
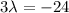
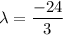
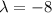
Therefore, from equation (2)

`x=2 +( \lambda )/(2)`

`x=2 +( -8 )/(2)`

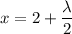
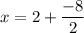
x = 2 - 4

x = - 2

From equation (3)

`x=4 +( \lambda )/(2)`

`x=4 +( -8 )/(2)`

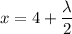
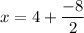
x = 4 - 4

x = 0

From equation (3)

`x=6 +( \lambda )/(2)`

`x=6 +( -8 )/(2)`

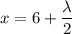
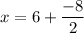
x = 6 -4

x = 2

i.e (x,y,z) = (-2, 0, 2)

∴

`d^2 = (x-2)^2 +(y-4)^2 + (z -6)^2`

`d^2 = (-2-2)^2 +(0-4)^2 + (2 -6)^2`

`d^2 = 16 +16 + 16`

`d^2 =48`

`d =√(48)`

`d= \pm 6.928`

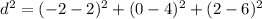
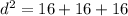
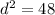
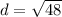
since we are taking only the positive integer because distance cannot be negative, then:

The distance from the center of the sphere to the plane is 6.928.

However, the distance from the surface S to the plane is:

6.928 - radius of the sphere.

where;

the radius of the sphere is given as 1

Then:

the distance from the surface S to the plane is:

6.928 - 1

= 5.928