Question

A girl rolls a ball up an incline and allows it to return to her. For the angle and ball involved, the acceleration of the ball along the incline is constant at 0.19g, directed down the incline. If the ball is released with a speed of 5.9 m/s, determine the distance s it moves up the incline before reversing its direction and the total time t required for the ball to return to the child's hand.

Answer 1

a) the distance the ball moves up the ramp is approximately 9.35 meters

b) the tme required for the ball to return to the girls' hands is 6.34 seconds

Step-by-step explanation:

The movement of the ball can be describe by a rectilinear movement with constant (negative) acceleration of 0.19 g = 1.862 m/s^2

Therefore the kinematic equations for the case the girl launches the ball at 5.9 m/s, we can write:

`x_f-x_i=5.9 \,t\,-(1.862)/(2) \,t^2=5.9\,t-0.931\,t^2\\and\\v_f=v_i-1.862\,t`

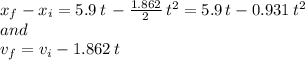
We use the second equation above to find the time it takes for the velocity to reduce to zero (and start the movement back down the ramp), and then use the time found to calculate the distance;

`v_f=v_i-1.862\,t\\0=5.9-1.862\,t\\t=(5.9)/(1.862) \\t=3.17\,\,s`

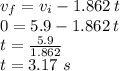
We use this time to find the distance the ball moves up the ramp:

`x_f-x_i=5.9\,t-0.931\,t^2\\distance=5.9\,(3.17)-0.931\.(3.17)^2=9.347\,\,m`

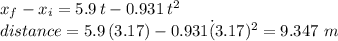
so the distance the ball moves up the ramp is approximately 9.35 meters

The ball will return to the hands of the girl in the double of the time it took to reach the max distance, that is 2 times 3.17 sec = 6.34 sec