Question

Vectors A, B, C and D have the following components:

X components (A, B, C and D respectively): +2.5 units, +6.1 units, -3.6 units and -1.5 units
Y components (A, B, C and D respectively): +4.3 units, -2.1 units, +1.0 units and -7.3 units

The magnitude of the resultant is:________

Answer 1

The magnitude of the resultant is approximately 5.391 units.

Step-by-step explanation:

We notice that vectors have the following characteristics: A magnitude and direction. That is:

`\vec v = r\cdot (\cos \theta\,\hat{i}+\sin \theta \,\hat{j})`

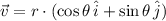
Where:

`r` - Magnitude, dimensionless.

`\theta` - Direction, measured in radians.

This expression can be rearranged as:

`\vec v = r\cdot \cos \theta \,\hat{i}+r\cdot \sin \theta \,j`

`\vec v = v_(x)\,\hat {i}+v_(y)\,\hat{j}`

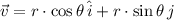
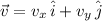
Where:

`v_(x) = r\cdot \cos \theta`

`v_(y) = r\cdot \sin \theta`

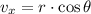
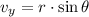
If we know a set of vectors of the form
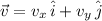`\vec {v} = v_(x)\,\hat{i}+v_(y)\,\hat{j}`, the resultant vector (
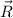`\vec {R}`) is the vectorial sum of every vector in the set:

`\vec{R} = \Sigma_(i=1)^(n) v_(i,x)\,\hat{i}+\Sigma_(i=1)^(n)v_(i,y) \,\hat{j}`

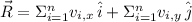
If we know that
`\vec{A} = 2.5\,\hat{i}+4.3\,\hat{j}`,
`\vec {B} = 6.1\,\hat{i}-2.1\,\hat{j}`,
`\vec C = -3.6\,\hat{i}+1.0\,\hat{j}` and
`\vec{D} = -1.5\,\hat{i}-7.3\,\hat{j}`, the resultant vector is:

`\vec {R} = \vec {A}+\vec {B} + \vec {C} + \vec {D}`

`\vec {R}=(2.5+6.1-3.6-1.5)\,\hat{i} + (4.3-2.1+1.0-7.3)\,\hat{j}`

`\vec {R} = 3.5\,\hat{i} -4.1\,\hat{j}`

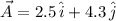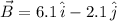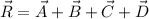
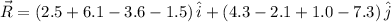
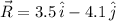
And lastly, we obtain the magnitude of the resultant by Pythagoras' Theorem:

`\|\vec R\| = \sqrt{3.5^(2)+(-4.1)^(2)}`

`\|\vec {R}\| \approx 5.391`

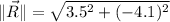
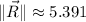
The magnitude of the resultant is approximately 5.391 units.