Answer:
20 kilometers
Explanation:
Mario will form a right triangle. The legs of the right triangle will be 16 and 12, from the 16 kilometers west and 12 kilometers south he walked.
Since it is a right, triangle, we can use the Pythagorean Theorem.

where
 and
and
 are the legs and
are the legs and
 is the hypotenuse.
is the hypotenuse.
We know that 16 and 12 are the legs. h will be the hypotenuse.
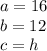
Substitute the values into the formula.
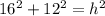
Now we must solve for
 by isolating it. First, evaluate the exponents on the left side.
by isolating it. First, evaluate the exponents on the left side.
⇒ 16²=16*16=256

⇒12²=12*12=144

Add 256 and 144.
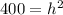
 is being squared. The inverse of a square is the square root. Take the square root of both sides of the equation.
is being squared. The inverse of a square is the square root. Take the square root of both sides of the equation.
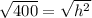
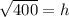
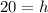
h= 20 km
The value of h is 20 kilometers.