Answer:
1. In the multiplication of the imaginary parts, the student forgot to square of i. OR
2. The student has only multiplied the real parts and the imaginary parts.
Correct value
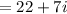 .
.
Explanation:
The given expression is
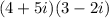
A student multiplies (4+5i) (3-2i) incorrectly and obtains 12-10i.
Student's mistake can be either 1 or second:
1. In the multiplication of the imaginary parts, the student forgot to square of i.
2. The student has only multiplied the real parts and the imaginary parts.
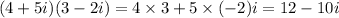
Which is not correct. The correct steps are shown below.
Using distributive property, we get
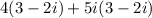
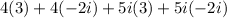
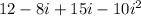

![[\because i^2=-1]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7zkfp9fycbczp657j2ujjh7ygl4k1wk7qx.png)
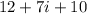
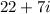
Therefore, the correct value of
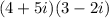 is
is
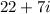 .
.