Question

A circle has a radius of 3.88 inches. Using the correct number of significant digits, find the circumference and area of the circle. The circumference is _____ in. The area is _____ in.

Answer 1

The circumference of the circle is 24.37 in

The area of the circle is 47.27 in²

Explanation:

The circumference of a circle is given by the formula

`C = 2\pi r\\`

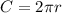
Where
`C` is the circumference of the circle

`\pi` is a constant (Take
`\pi` = 3.14)

and
`r` is the radius of the circle

From the question,

radius,
`r` = 3.88 in

Hence, the circumference,
`C` becomes

`C = 2\pi r\\`

`C = 2(3.14)(3.88)\\`

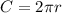
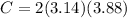
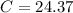`C = 24.37` in

Hence, the circumference of the circle is 24.37 in

For the area of the circle,

Area of a circle is given by

`A = \pi r^(2)`

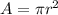
Where
`A` is the area of the circle

Since, radius,
`r` = 3.88 in

The area of the circle then becomes

`A = \pi r^(2)`

`A = (3.14) (3.88)^(2)`

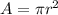
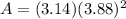
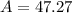`A = 47. 27` in²

Hence, the area of the circle is 47.27 in²