Question

I need help in this question

Answer 1

`x = 4`

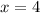
m∠EFH = 21°

m∠EFG = 83°

Explanation:

We know that m∠EFH + m∠HFG will be equal to m∠EFG.

Since we know the values of each, we can make the equation:

`5x + 1 + 62 = 18x + 11`

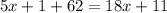
Let's solve for x by isolating it on one side.

Combine like terms:

`5x + 63 = 18x + 11`

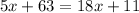
Subtract 11 from both sides:

`5x + 52 = 18x`

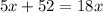
Subtract 5x from both sides:

`52 = 13x`

Divide both sides by 13:

`x = 4`

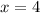
Now that we know the value of x, we can substitute it inside the formulas for m∠EFH and m∠EFG.

m∠EFH:

`5x+1\\\\5(4)+1\\\\20+1\\\\21`

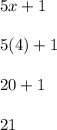
m∠EFG:

`18x+11\\\\18(4)+11\\\\72+11\\\\83`

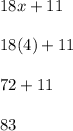
Hope this helped!