Answer:
The velocity of the particle is given by
 , where
, where
 is in meters per second and
is in meters per second and
 is in seconds.
is in seconds.
The displacement of the particle is given by
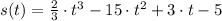 , where
, where
 is in meters and
is in meters and
 is in seconds.
is in seconds.
Step-by-step explanation:
The acceleration of the particle is given by
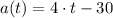 , the expression for velocities are obtained by integration:
, the expression for velocities are obtained by integration:
Velocity

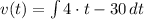
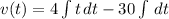
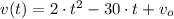
Where
 is the initial velocity of the particle, measured in meters per second.
is the initial velocity of the particle, measured in meters per second.
If
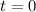 and
and
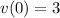 , then:
, then:
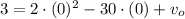

The velocity of the particle is given by
 , where
, where
 is in meters per second and
is in meters per second and
 is in seconds.
is in seconds.
Displacement
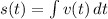
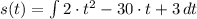
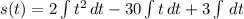
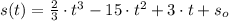
If
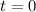 and
and
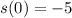 , then:
, then:
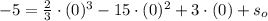

The displacement of the particle is given by
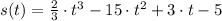 , where
, where
 is in meters and
is in meters and
 is in seconds.
is in seconds.