Question

A metallurgist needs to make 12 oz. Of an alloy containing 45% copper. He is going to melt and combine one metal that is 30% copper with another metal that is 50% copper. How much of each should he use?

Answer 1

The metallurgist should use 3 ounces of the 30 % copper alloy and 9 ounces of the 50 % copper alloy to make 12 ounces of 45 % copper alloy.

Explanation:

The ounce is a mass unit, as we notice that the metallurgist wants to make 12 ounces of an alloy containing 45 % copper by mixing two metal with different copper proportions. We can use the following two equations:

Alloys

`m_(R) = m_(A)+m_(B)` (Eq. 1)

Copper

`r_(R)\cdot m_(R) = r_(A)\cdot m_(A)+r_(B)\cdot m_(B)` (Eq. 2)

Where:

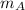`m_(A)` - Mass of the 30 % copper alloy, measured in ounces.

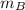`m_(B)` - Mass of the 50 % copper alloy, measured in ounces.

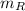`m_(R)` - Mass of the 45 % copper alloy, measured in ounces.

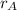`r_(A)` - Proportion of copper in the 30 % copper alloy, dimensionless.

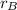`r_(B)` - Proportion of copper in the 50 % copper alloy, dimensionless.

`r_(R)` - Proportion of copper in the 45 % copper alloy, dimensionless.

Now, the mass of the 50 % copper alloy is cleared in Eq. 1 and eliminated in Eq. 2:

`r_(R)\cdot m_(R) = r_(A)\cdot m_(A) + r_(B)\cdot (m_(R)-m_(A))`

`(r_(R)-r_(B))\cdot m_(R) = (r_(A)-r_(B))\cdot m_(A)`

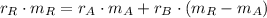
And we clear and calculate the mass of the 30 % copper alloy:

`m_(A) = m_(R)\cdot \left((r_(R)-r_(B))/(r_(R)-r_(A)) \right)`

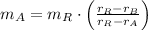
If we know that
`m_(R) = 12\,oz`,
`r_(R) = 0.45`,
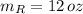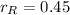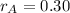`r_(A) = 0.30` and
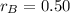`r_(B) = 0.50`, the mass of the 30 % copper alloy:

`m_(A) = (12\,oz)\cdot \left((0.45-0.50)/(0.30-0.50) \right)`

`m_(A) = 3\,oz`

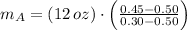
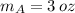
And the mass of the 50 % copper alloy is:

`m_(B) = m_(R)-m_(A)`

`m_(B) = 12\,oz-3\,oz`

`m_(B) = 9\,oz`

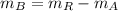
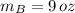
The metallurgist should use 3 ounces of the 30 % copper alloy and 9 ounces of the 50 % copper alloy to make 12 ounces of 45 % copper alloy.