Question

Rewrite in simplest radical form: x^4/5 / x^1/3 into a√x^b

Answer 1

`\sqrt[15]{x^7}`

Explanation:

If we have the expression

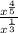`\frac{x^{(4)/(5)}}{x^{(1)/(3)}}`, we have to think about exponent rules.

If we have
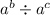`a^b / a^c`, then the value will be equal to
`a^(b-c)`.

So
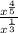`\frac{x^{(4)/(5)}}{x^{(1)/(3)}}` simplified will be
`x^{(4)/(5) - (1)/(3)}`

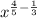
Converting
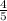`(4)/(5)` and
`(1)/(3)` into fifteenths (lcm) gets us
`(12)/(15) - (5)/(15) = (7)/(15)`.

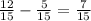We can convert
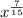`x^{(7)/(15)}` into a radical by taking the denominator root of x to the numerator.

`\sqrt[15]{x^7}`.

Hope this helped!