Question

You wish to assess, approximately, the thermal conductivity λ of polyethylene (PE). To do so you block one end of a PE pipe with a wall thickness of x = 3 mm and diameter of 30 mm and fill it with boiling water while clutching the outside with your other hand. You note that the outer surface of the pipe first becomes appreciably hot at a time t ≈ 18 seconds after filling the inside with water. Use this information, plus data for specific heat C p and density rho of PE, to estimate λ for PE. How does your result compare with the listed value in the CES EduPack?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The value is
`\lambda  =  0.44 \  W/mK`

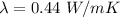
The calculated value is greater than the value from the CES EduPack

(A picture of the listings of the CES EduPack is shown on the second uploaded image )

Step-by-step explanation:

From the question we are told that

The distance x that the heat diffuses in the time t is approximately

`x =  √(2 at)`

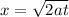
Where

`a =  (lambda )/(\rho *  C_p)`

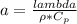
Now from the question we know that t = 18 s and x = 3mm = 0.003 m,
`C_p  =  1850 \  J/kg/K`

So

`0.003 =  √(2 *  a  *  18 )`

=>
`a =  (9*10^(-6))/(36)`

=>
`a =  2.5*10^(-7)`

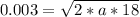
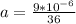
Generally the density of the polyethylene is
`\rho =  950 kg/m^3`

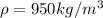
So

`2.5*10^(-7)  =  (\lambda )/(950 *  1850)`

=>
`\lambda  =  0.44 \  W/mK`

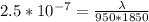
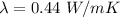
From the CES EduPack the value listed for thermal conductivity λ of polyethylene is

`0.113 \to 0.167 \ W/mK`

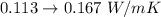
So the calculated value is greater that the value from the CES EduPack