Answers:
7) Center= (-1,2) Radius=
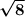 Equation:
Equation:
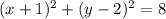
8) Center= (3,13) Radius= 13 Equation:
=========================================================
Step-by-step explanation:
Problem 7
Let's find the distance from (-1,2) to (-3,4)
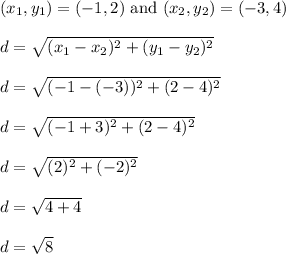
This is the radius because it stretches from the center to a point on the circle, so
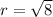
Squaring both sides will get us
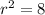
One useful template for a circle is the equation
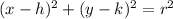
(h,k) is the center
r is the radius
Let's plug in the given center (h,k) = (-1,2) and the r^2 value we found earlier.
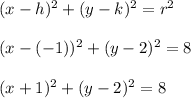
You can confirm this by using a tool like Desmos. See below.
------------------------------------------------------------------------
Problem 8
The endpoints of the diameter are (-2,1) and (8,25)
The center is the midpoint of these endpoints.
The midpoint of the x coordinates is (-2+8)/2 = 3
The midpoint of the y coordinates is (1+25)/2 = 13
The center is (h,k) = (3,13)
Now find the distance from the center to one of the points on the circle, let's say to (8,25)
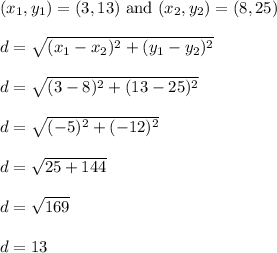
The radius is exactly 13 units.
So,
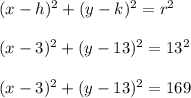
is the equation of this particular circle.
Visual confirmation is shown below.