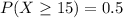Question

The manufacturer of an electronic device claims that the probability of the device failing during the warranty period is 0.005. If 3000 of these devices are sold, the probability that at least 15 of them fail during the warranty period is closest to :_________

Answer 1

The value is
`P(X \ge 15) = 0.5`

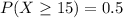
Explanation:

From the question we are told that

The probability of the device failing during the warranty period is
`p = 0.005`

The sample size is
`n = 3000`

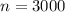
The random variable considered is x = 15

Generally this is distribution is binomial given the fact that there is only two out comes hence

X which is a variable representing a randomly selected selected electronic follows a binomial distribution i.e

`X \~ \ B(n , p)`

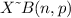
Now the mean is mathematically evaluated as

`\mu = n * p`

=>
`\mu = 3000 * 0.005`

=>
`\mu =15`

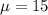
The standard deviation is mathematically represented as

`\sigma = √(np(1 -p ))`

=>
`\sigma = √(3000 * 0.005 * (1 - 0.005 ))`

=>
`\sigma = 3.86`

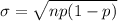
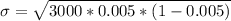
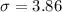
Now given that n is very large, then it mean that we can successfully apply normal approximation on this binomial distribution

So

`P(X \ge 15) = P( (X - \mu)/(\sigma ) \ge (x - \mu)/(\sigma ) )`

Now applying Continuity Correction we have

`P(X \ge (15-0.5)) = P( (X - \mu)/(\sigma ) > ((15 -0.5) - 15)/(3.86 ) )`

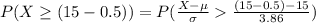
Generally
`(X - \mu)/(\sigma ) = Z (The \ standardized \ value \ of \ X)`

`P(X \ge (15-0.5)) = P(Z >-0.130 )`

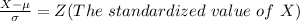
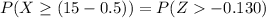
From the z-table

`P(Z >-0.130 ) =0.5`

Thus

`P(X \ge 15) = 0.5`