Answer:
1)
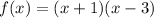
2)
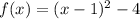
3)
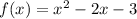
Explanation:
So we have a graph and we know that its roots are at x=-1 and x=3.
We also know the vertex is at (1,-4). With that, we can figure out the three forms.
Factored Form:
The factored form, as given, is:

We already know the roots of -1 and 3. So, substitute:
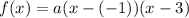
Simplify:
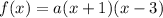
Now, we just need to figure out a. To do so, we can use the vertex. Since the vertex is at (1,-4), this means that f(1) is -4. So, substitute 1 for x and substitute -4 for f(x):

Add and subtract:
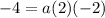
Multiply:
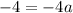
Divide both sides by -4:
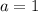
So, our factored form is:
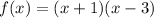
Vertex Form:
The vertex form is:
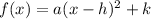
Where (h,k) is the vertex.
We already know the vertex is (1,-4), so substitute 1 for h and -4 for k.
We also previously determined that a is 1, so substitute that also. So:
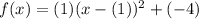
Simplify:
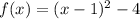
Standard Form:
To acquire the standard form, simply expand the factored or vertex form. I'm going to expand the factored form:
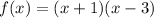
FOIL:
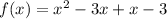
Combine like terms:
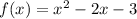
And we're done!