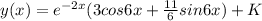Question

Solve the initial value problem y′′+4y′+40y=0y(0)= 3y′(0)=5.

Answer 1

`y(x) =e^(-2 x)(3cos6 x + (11)/(6) sin6 x) + K`

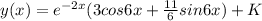
Explanation:

Given the initial value problem y′′+4y′+40y=0 where y(0)= 3 and y′(0)=5.

Find the solution in the attached file.

Since the solution is a complex number, the solution to the second order differential equation is given as shown;

y(x) =
`e^(\alpha x)(c_1cos\beta x + c_2sin \beta x)`

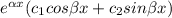
from the complex solution D = -2+6i

`\alpha = -2, \beta = 6`

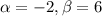
y(x) =
`e^(-2 x)(c_1cos6 x + c_2sin6 x)`

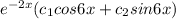
Substituting the initial values

when y(0) = 3, the solution becomes;

`3 = e^(-2 x)(c_1cos6 (0) + c_2sin 6 (0))\\`

`3 = e^(-2 (0))(c_1+ 0)\\3 = 1*c_1\\c_1 = 3`

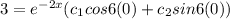
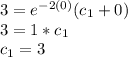
From y(x) =
`e^(\alpha x)(c_1cos\beta x + c_2sin \beta x)`

`y'(x) = e^(\alpha x)(-\beta c_1sin\beta x + \beta c_2cos \beta x)+\alpha e^(\alpha x)(c_1cos\beta x + c_2sin \beta x)`

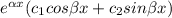
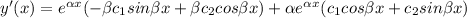
at y'(0) = 5, the solution becomes;

`y'(x) = e^(\alpha x)(-\beta c_1sin\beta x + \beta c_2cos \beta x)+\alpha e^(\alpha x)(c_1cos\beta x + c_2sin \beta x)\\5 = e^(-2 (0))(-6 c_1sin6 (0) + 6 c_2cos 6 (0))+-2 e^(-2 (0))(c_1cos6 (0) + c_2sin 6 (0))\\5 = 1*(0 + 6 c_2)-2(c_1 + 0)\\5 = 6c_2-2c_1`

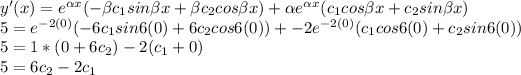
Since c₁ = 3;

5 = 6c₂ - 2(3)

5 = 6c₂ - 6

6c₂ = 11

c₂ = 11/6

Substituting the constant into the solution to the differential equation
`y(x) =e^(-2 x)(c_1cos6 x + c_2sin6 x)`

`y(x) =e^(-2 x)(3cos6 x + (11)/(6) sin6 x) + K`