Question

Point C is in the interior of ∠ABD, and ∠ABC ≅ ∠CBD. If m∠ABC = 5/2x + 18) and m∠CBD = (4x), what is m∠ABD?

Answer 1

m∠ABD = 96

Explanation:

Given

m∠ABC = 5/2x + 18

m∠CBD = 4x

Required

Determine m∠ABD

From the given parameters, we understand that:

∠ABC ≅ ∠CBD

This implies that:

`(5)/(2)x + 18 = 4x`

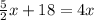
Collect Like Terms

`(5)/(2)x - 4x =- 18`

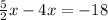
Take LCM

`(5x - 8x)/(2) = -18`

`(-3x)/(2) = -18`

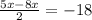
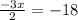
Cross Multiply

`-3x = -18 * 2`

`-3x = -36`

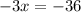
Divide through by -3

`x = 12`

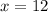
m∠ABD can be calculated using:

m∠ABD = m∠ABC + m∠CBD

`ABD = (5)/(2)x + 18 + 4x`

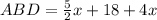
Substitute 12 for x

`ABD = (5)/(2) * 12 + 18 + 4 * 12`

`ABD = 30 + 18 + 48`

`ABD = 96`

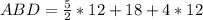
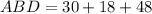
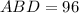
Hence;

m∠ABD = 96