Question

The volume of a cube is
`27n^(27)`. What is the length of one side of the cube?

Answer 1

The answer is

`{3n}^(9)`

Explanation:

Volume of a cube = l³

where

l is the length of one side

From the question the volume is
`{27n}^(27)`

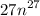
The length of one side is

`{l}^(3) = {27n}^(27)`

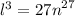
Find the cube root of both sides

That's

`l = \sqrt[3]{ {27n}^(27) }`

Write the equation in exponent form

That's

`\sqrt[3]{ {3}^(3) {n}^(27) }`

But

`\sqrt[3]{x} = {x}^{ (1)/(3) }`

So we have

`( { {3}^(3) {n}^(27) })^{ (1)/(3) } = {3}^{3 * (1)/(3) } * {n}^{27 * (1)/(3) }`

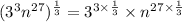
We have

`3 * {n}^(9)`

So we have the final answer as

`{3n}^(9)`

Hope this helps you