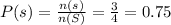Question

A silver dollar is flipped twice. Calculate the probability of each of the following occurring: a head on the first flip a tail on the second flip given that the first toss was a head two tails a tail on the first and a head on the second a tail on the first and a head on the second or a head on the first and a tail on the second at least one head on the two flips

Answer 1

Explained below.

Explanation:

The sample space for flipping a dollar twice is:

S = {HH, HT, TH, TT}

n (S) = 4

Independent events are those events that does not affect each other.

In this case, the outcomes of the two tosses are independent, i.e. the outcome of the second toss does not depends on the second toss.

(1)

Compute the probability of a head on the first flip:

The favorable outcomes are:

H₁ = {HH, HT}

n (H₁) = 2

`P(H_(1))=(n(H_(1)))/(n(S))=(2)/(4)=(1)/(2)=0.50`

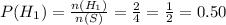
(2)

Compute the probability of a tail on the second flip given that the first toss was a head:

The favorable outcomes are:

T₂ | H₁ = {HT}

n (T₂ | H₁) = 1

`P(T_(2)|H_(1))=(n(T_(2)|H_(1)))/(n(H_(1)))=(1)/(2)=0.50`

(3)

Compute the probability of two tails:

T₁ and T₂ = {TT}

n (T₁ and T₂) = 1

`P(T_(1)\cap T_(2))=(n(T_(1)\cap T_(2)))/(n(S))=(1)/(4)=0.25`

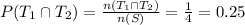
(4)

Compute the probability of a tail on the first and a head on the second:

T₁ and H₂ = {TH}

n (T₁ and H₂) = 1

`P(T_(1)\cap H_(2))=(n(T_(1)\cap H_(2)))/(n(S))=(1)/(4)=0.25`

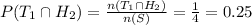
(5)

Compute the probability of at least one head on the two flips:

s = {HH, HT, TH}

n (s) = 3

`P(s)=(n(s))/(n(S))=(3)/(4)=0.75`