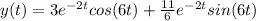Answer:
The solution is
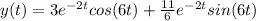
Explanation:
First we will write the characteristic equation, which is
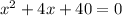
This is a quadratic equation
For the general form of quadratic equation,
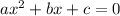 ,
,
 is given by the general formula,
is given by the general formula,
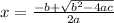 or
or
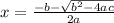
Hence, for
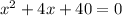
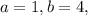 and
and
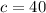
Hence, the formula becomes
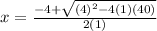 or
or
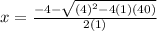
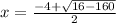 or
or
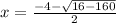
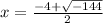 or
or
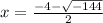
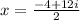 or
or
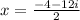
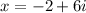 or
or
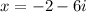
Hence,
 ±
±
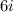
That is,
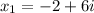 or
or
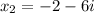
These are the roots of the equation.
For the general solution,
Since the roots of the equation are complex,
If the roots of a characteristic equation are in the form
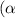 ±
±
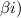 , then the general solution is given by
, then the general solution is given by
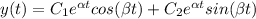
Hence, the general solution for the differential equation becomes
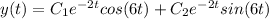
Then
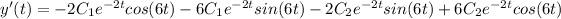
Now, from the question,
y(0)= 3
y′(0)=5.
That is,
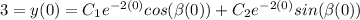
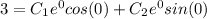
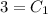
∴
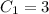
[NOTE:
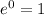 and
and
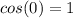 and
and
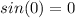 ]
]
Also,
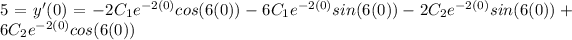
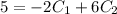
Now, we can find
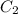 by putting the value of
by putting the value of
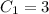 into the equation
into the equation
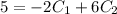
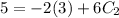
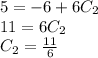
∴
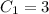 and
and
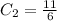
Then the solution becomes