Question

A farmer applies 1300.0 kg of a fertilizer that contains 10.0% nitrogen to his fields each year. Fifteen (15.0%) percent of the fertilizer washes into a river that runs through the farm. If the river flows at an average rate of 0.460 cubic feet per second, what is the additional concentration of nitrogen (expressed in milligrams of nitrogen per liter) in the river water due to the farmer's fertilizer?

Answer 1

the additional concentration of nitrogen = 0.04748 mg/L

Step-by-step explanation:

From the given information:

The mass of the nitrogen added to the field per year = 10% of 1300.0 kg

=
`(10)/(100) * 1300`

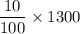
= 130 kg

The mass of the nitrogen that is being also washed into the river

= 15% of 130 kg

=
`(15)/(100) * 130`

= 15 × 1.3 kg

= 19.5 kg /year

Converting kg/year into milligram per seconds; we have:

`(19.5 * 10^6 \ mg)/(365 * 3600*24 \ seconds )`

= 0.61834 mg/seconds

If the river flows at an average rate of 0.460 cubic feet

Let's convert the cubic feet into liters

we all know that;

1 ft = 0.33 meter

1 cubic feet = 28.31 liters

∴ 0.460 cubic feet = 0.460 × 28.31

13.0226 liters

Finally, the additional concentration of nitrogen =
`(0.61834)/(13.0226 )`

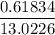
the additional concentration of nitrogen = 0.04748 mg/L