Question

Do there exists nonhomeomorphic closed sets?

Answer 1

yes,

Explanation:

Homeomorphic sets :-

Two sets are homeomorphic if define a function f between both sets which is satisfy the following conditions:

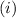`(i)` Function f is a bijection (one-to-one and onto),

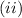`(ii)` Function f is continuous,

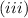`(iii)` Inverse function of f is also continuous.

example:

Let
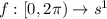`f:[0, 2\pi)\rightarrow s^1`given by
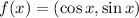`f(x)=(\cos x, \sin x)` where
`f(x)` is a continuous and bijection fuction but inverse of fuction f is discontinuous.

Hence, set
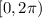`[0,2\pi)` and
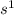`s^1` are not homeomorphic.