Question

A group of 8 students apply for MBA program at CBA, CSULB. According to the historical data, probability of admittance at MBA program is .65. Using the formula and showing all work and steps, compute the followings:

Probability for the following number of students to get admitted:

3, 2, 1, 0

Probability of at least 4 students get admitted

Expected value of the discrete probability

Standard deviation

Answer 1

Probability = 0.894

Expected value = 5.2

Standard deviation = 1.349

Explanation:

Given that

p = 0.65

n = 8

q = 1 - p

= 1 - 0.65

= 0.35

`P(x) = ^n(c_x)* P^x* q^(n-x)`

For P(3)

`= ^8c_3* 0.65^3* 0.35^5`

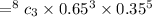
Which gives result

= 0.0808

For P(2)

`= ^8c_2* 0.65^2* 0.35^6`

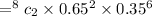
Which gives result

= 0.0217

For P(1)

`= ^8c_1* 0.65^1* 0.35^7`

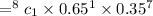
which gives result

= 0.0033

For P(0)

`= 0.35^8`

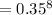
= 0.0002

Now probability is at least getting admitted of 4 students

= 1 - {P(3) + P(2) + P(1) + P(0)}

= 1 - (0.0808 + 0.0217 + + 0.0033 + 0.0002)

= 1 - 0.106

= 0.894

Expected value =
`n* p`

`= 8* 0.65`

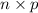
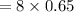
= 5.2

Standard deviation

`= √(n* p* q) \\\\\ = √(8* 0.65* 0.35)`

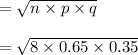
= 1.349