Question

Find the point of intersection of the given plane (y = −17) and the line that is perpendicular to the given plane and passes through (4, 8, 3).

Answer 1

The point of intersection is
`\left[\begin{array}{c}4&-17&3\end{array}\right]`

Explanation:

In order to find the intersection point we will need to find the vector equation of the line.

The plane equation is
`y=-17`

Now to find the line that is perpendicular to this plane, we can do the following reasoning :

The plane and the line will be perpendicular between each other if and only if the direction vector of the line is a scalar multiple from the normal vector of the plane.

The plane equation is
`y=-17`. Then any vector with the following form :

`\left[\begin{array}{c}0&a&0\end{array}\right]`

With
`a` ∈ IR ,
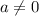`a\\eq 0` will be perpendicular to the plane.

Let's choose
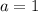`a=1` to simplify the calculations.

The normal vector of the plane is
`\left[\begin{array}{c}0&1&0\end{array}\right]`

Now the direction vector of the line must be a scalar multiple of this vector ⇒
`V=b\left[\begin{array}{c}0&1&0\end{array}\right]` ,
`b` ∈ IR

Let's also choose
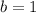`b=1` in order to simplify the calculations.

The vectorial equation of the line is :

`\left[\begin{array}{c}x&y&z\end{array}\right]=\alpha V+P` with
`\alpha` ∈ IR

Where
`V` is the direction vector and
`P` is any point where the line passes through.

Using the data from the question we complete our equation with :

`IL=\left[\begin{array}{c}x&y&z\end{array}\right]=\alpha\left[\begin{array}{c}0&1&0\end{array}\right]+\left[\begin{array}{c}4&8&3\end{array}\right]` with
`\alpha` ∈ IR

Now let's find the intersection point between the plane
`y=-17` and the line
`IL`

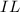
This intersection point must belong to the line and also to the plane.

In order to belong to the plane its second component must be
`-17`

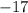
Knowing this and using the vector equation of the line we obtain this equation :

`\alpha +8=-17` ⇒
`\alpha =-25`

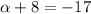Using
`\alpha =-25` in the vector equation of the line we find that the point is

`\left[\begin{array}{c}4&-17&3\end{array}\right]`

This point belongs to the plane (because its second component is
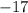`-17`) and also to the line (because it can be obtained using the vector line equation with
`\alpha =-25`).