Question

. Assume that you are considering the purchase of a 80-year, noncallable bond with an annual coupon rate of 9.5%. The bond has a face value of $1,000, and it makes semiannual interest payments. If you require an 9.7% nominal yield to maturity on this investment, what is the maximum price you should be willing to pay for the bond?

Answer 1

Answer: $982.48

Explanation:

The maximum price you should pay would be the present value of the bond including its cash flows. That is how the price of a bond is computed.

The formula to calculate the price of a bond is;

`Price = Coupon payment * (1 - (1 + yield)^(-n) )/(yield) + (Future value)/(( 1 + r) ^n)`

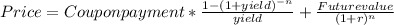
The payments are semi annual so the variables will need to be converted to semi annual variables.

Coupon payment = 9.5% * 1,000 * 1/2

= $47.50

Number of periods = 20 years * 2 = 40 semi annual periods

Yield = 9.7%/2 = 4.85%

`Price = 47.50 * (1 - (1 + 0.0485)^(-40) )/(0.0485) + (1,000)/(( 1 + 0.0485)^(40) )\\Price = 832.077 * 150.405\\Price = 982.48`

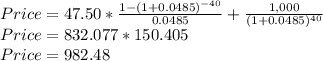
Price = $982.48

$982.48 should be the maximum price you should pay.

Alternatively, use a financial calculator and input the variables as;

Future Value = $1,000

Payment = $47.50

Number of Periods = 40

Rate = 4.85%