Question

BD bisects ABC so that ABD = 2y and CBD = 5y – 12.

Answer 1

`y = 4`

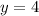
Explanation:

Given

`ABD = 2y`

`CBD = 5y - 12`

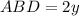
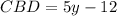
Required

Find y ---Missing part of the question

Since BD bisects ABC;

This implies that

`ABD = CBD`

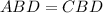
This is so because a bisector splits a segment into equal parts;

Substitute values for ABD and ABC

`2y = 5y - 12`

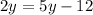
Collect Like Terms

`2y - 5y= - 12`

`-3y = -12`

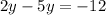
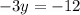
Divide both sides by -3

`y = 4`

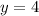
Hence;

The value of y is 4