Answer:
See Explanation
Explanation:
The question is incomplete because the coordinates of A, B and C were not given in the question.
However, the following explanation will guide you...
The midpoints, C of two point A and B is calculated as:
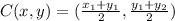
Where
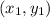 are the coordinates of A
are the coordinates of A
and
 are the coordinates of B
are the coordinates of B
Take for instance, the given coordinates are
A(4,6); B(2,4) and C(3,5)
Then;
Plug in these values in the given formula:
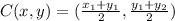

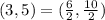
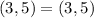
In that case,
C is really the midpoint
To the b part: Explaining why ratio 1:1 is used
The reason is that both parts of the ratio are in equal proportion (1 and 1);
Because of this equal proportion, ration 1:1 is right to calculate the midpoint