Question

Lines l and m are parallel. If m∠3 = 3x + 11 degrees and m∠2 = 4x + 1 degrees, what is the measure of ∠7? 41 degrees 139 degrees 180 degrees

Answer 1

m<7 = 139°

Explanation:

Given:

m<3 = (3x + 11)°

m<2 = (4x + 1)°

Required:

m<7 = ?

SOLUTION:

Given that l and m are parallel lines, m<3 and m<2 are alternate interior angles.

Alternate interior angles are congruent. Therefore:

m<3 = m<2

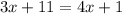`3x + 11 = 4x + 1` (substitution)

Solve for x

`3x + 11 - 4x = 4x + 1 - 4x`

`-x + 11 = 1`

`-x + 11 - 11 = 1 - 11`

`-x = -10`

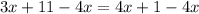
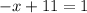
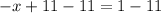
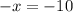
Divide both sides by -1

`x = 10`

Find m<2:

m<2 = (4x + 1)

Plug in the value of x

m<2 = 4(10) + 1 = 40 + 1

m<2 = 41°

Find m<7:

m<2 + m<7 = 180° (consecutive interior angles are supplementary)

41° + m<7 = 180° (substitution)

m<7 = 180 - 41 (subtracting 41 from each side)

m<7 = 139°