Question

The string of a kite is 120 metres long and it makes an angle of 60 degree

the horizontal. Find the height of the kite from the ground, assuming the
a w
there is no slack in the string.​

Answer 1

103.92 m

Explanation:

The kite is making right angle with the ground and its string is acting as hypotenuse of right triangle.

Let the height of the kite from the ground be h meters.

Therefore, by trigonometrical ratio:

`\sin \theta \: = (height \: of \: the \: kite)/(length \: of \: the \: string) \\ \\ \sin 60 \degree \: = (h)/(120) \\ \\ ( √(3) )/(2) = (h)/(120) \\ \\ h = ( √(3) )/(2) * 120 \\ \\ h = √(3) * 60 \\ \\ h = 1.732 * 60 \\ \\ h = 103.92 \: m \\`

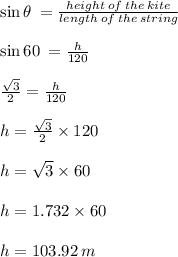
Thus, the height of the kite from the ground is 103.92 meters.