Question

Three positive integers a, b and c have, in pairs, highest common factors (a,b) = 24, (b,c) = 198 and (a,c) = 210. (a) What is the highest common factor of a, b and c? (b) Find the smallest values of a, b and c which satisfy the given criteria.

Answer 1

1584, 6930, and 840.

Explanation:

just trial and error lol

Answer 2

HCF(a,b,c)=6

Smallest values of a, b and c are 840, 792 and 6930 respectively.

Explanation:

It is given that,

HCF(a,b)=24, HCF(b,c)=198 and HCF(a,c)=210.

If means 24 and 210 are the factors of a.

`a=LCM(24,210)=840`

If means 24 and 198 are the factors of b.

`b=LCM(24,198)=792`

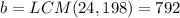
If means 198 and 210 are the factors of c.

`c=LCM(198,210)=6930`

Therefore, the smallest values of a, b and c which satisfy the given criteria are 840, 792 and 6930 respectively.

Now,

`HCF(a,b,c)=HCF(840,792,6930)=6`

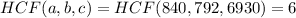
Therefore, HCF of a, b and c is 6.