Question

Help me pwease? very last minute

Answer 1

Let
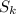`S_k` be the k-th partial sum of the infinite series,

`\displaystyle S_k = \sum_(n=1)^k \frac23 \left(\frac14\right)^(n-1) = \frac23 \left(1 + \frac14 + \frac1{4^2} + \cdots + \frac1{4^(k-1)}\right)`

Multiply both sides by 1/4 :

`\displaystyle \frac14 S_k = \frac23 \left(\frac14 + \frac1{4^2} + \frac1{4^3} + \cdots + \frac1{4^k}\right)`

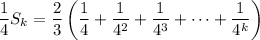
Subtract this from
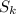`S_k` and solve for
`S_k` :

`\displaystyle S_k - \frac14 S_k = \frac23 \left(1 - \frac1{4^k}\right)`

`\displaystyle \frac34 S_k = \frac23 \left(1 - \frac1{4^k}\right)`

`\displaystyle S_k = \frac89 \left(1 - \frac1{4^k}\right)`

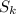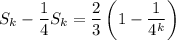
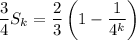
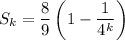
Then as k goes to infinity, the exponential term will converge to zero, and the sum will converge to

`\displaystyle S = \lim_(k\to\infty) S_k = \boxed{\frac89}`

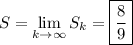
Generalizing this result, we have for |r| < 1,

`\displaystyle \sum_(n=1)^\infty a r^(n-1) = \frac a{1-r}`