Answer:
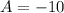 and
and

Explanation:
The given sphere is
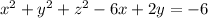
This can be rearranged as
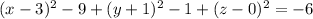
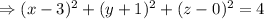
On comparing with the standard equation of a circle
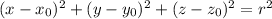 , with center
, with center
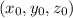 and radius
and radius
 .
.
The center of the given circle is
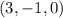 .
.
Now, as the perpendicular distance,
 , of a point
, of a point
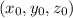 from a plane
from a plane
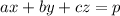 is
is
 .
.
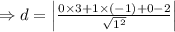 [ as the given plane is y=2]
[ as the given plane is y=2]
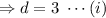
Similarly, the other equation of the circle,
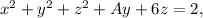 can be rearranged as
can be rearranged as
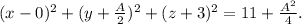
Here, the center for this circle is
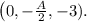
From the given condition, the distance of the center from the plane
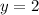 is
is
 .
.
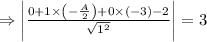 [from equation (i) ]
[from equation (i) ]


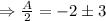
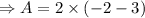 and
and
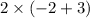
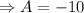 and
and
 .
.