Answer:
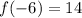
Explanation:
According to the remainder theorem, if a function f(x) is divided by (x-a), then the remainder is defined by f(a).
It is given that
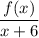 has a remainder of 14.
has a remainder of 14.
Here, the function f(x) is divided by (x+6). So, on comparing (x+6) and (x-a), we get
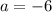
So, by remainder theorem, remainder of
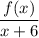 is f(-6).
is f(-6).
Since the remainder is 14, therefore
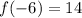
Therefore, the answer for first blank is -6 and for second blank is 14, i.e.,
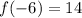 .
.