Answer:
The equation of the line is
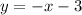 .
.
Explanation:
Let be
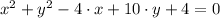 and
and
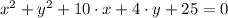 the general equations of the two circles, which must be transformed into their standard forms, which are:
the general equations of the two circles, which must be transformed into their standard forms, which are:
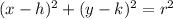
Where:
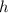 ,
,
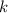 - Components of the center of the circle, dimensionless.
- Components of the center of the circle, dimensionless.
 - Radius of the circle, dimensionless.
- Radius of the circle, dimensionless.
1)
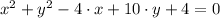
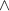
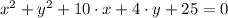 Given
Given
2)
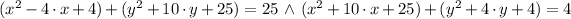 Associative property/Compatibility with addition
Associative property/Compatibility with addition
3)
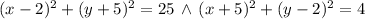 Perfect square trinomial/Result
Perfect square trinomial/Result
The centers of both circles are
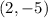 and
and
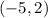 , respectively.
, respectively.
A line is represented by the following expression:
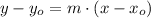
Where:
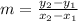
If
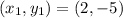 ,
,
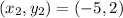 and
and
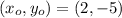 , the equation of the line is:
, the equation of the line is:
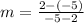
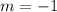
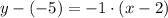
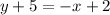
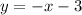
The equation of the line is
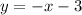 .
.