Complete Question
The complete question is shown on the first uploaded
Answer:
 is not a solution of the differential equation
is not a solution of the differential equation
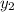 is not a solution of the differential equation
is not a solution of the differential equation
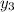 is not a solution of the differential equation
is not a solution of the differential equation
Explanation:
The differential equation given is
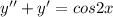
Let consider the first equation to substitute

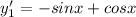
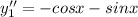
So
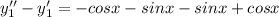
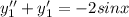
So

This means that
 is not a solution of the differential equation
is not a solution of the differential equation
Let consider the second equation to substitute
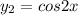
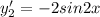
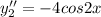
So
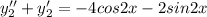
So
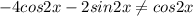
This means that
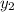 is not a solution of the differential equation
is not a solution of the differential equation
Let consider the third equation to substitute
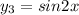

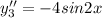
So

So
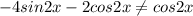
This means that
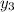 is not a solution of the differential equation
is not a solution of the differential equation