Answer:
The profit is
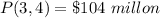
The number of solar panels of type a is 3 thousand
The number of solar panels of type B is 4 thousand
Explanation:
From the question we are told that
The revenue function is
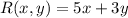
The cost function is
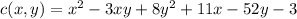
Generally the profit function is mathematically represented as
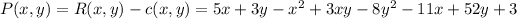
Now the next step is to differentiate the profit function partially
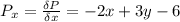

At maximum or minimum
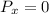 so
so
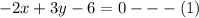
and
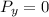
So
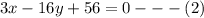
Solving equation 1 and 2 simultaneously using substitution method
From 1
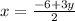
substituting this to 2
![3[(-6+3y)/(2) ] -16y + 56 = 0](https://img.qammunity.org/2021/formulas/mathematics/college/di1k0drpgiex2f62qb50ligx023z8j5nit.png)
multiply through by 2
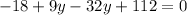
=>
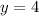
So
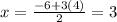
So the critical point is (v,w) = (3, 4)
Now differentiating
 partially and substituting the critical point s we have
partially and substituting the critical point s we have
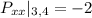
Now differentiating
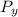 partially and substituting the critical point s we have
partially and substituting the critical point s we have

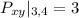
Now to determine whether the obtained critical point is maximum or minimum the expression
![D = P_(xx)|_(3,4) * P_(yy)|_(3,4) - [P_(xy)|_(3,4) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/93jlp887j6nqyneeiw7cey2p3ytsnle9nd.png) must be greater than zero so
must be greater than zero so

So \
The maximum price is mathematically evaluated as
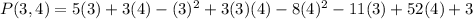
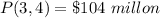
So
The number of solar panels of type a is 3 thousand
The number of solar panels of type B is 4 thousand