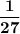Question

Consider a post office with two clerks. Three people: A, B, and C; enter simultaneously. A and B go directly to the two clerks, and C waits until either A or B leaves before beginning service with the free clerk. What is the probability A is the last customer to complete service when

Answer 1

(1) Pr(A > B + C) = 0

(2)
`\mathbf{(1)/(27)}`

Explanation:

From the information given:

What is the probability A is the last customer to complete service when:

(1) the service time for each clerk is precisely ten minutes?

The probability (Pr) that A is the last customer can be computed as:

P( A > B + C )

if we recall, we are being told that the service time for each clerk is 10 minutes. As such, there is no occurrence of any event.

Therefore, the probability A is the last customer to complete service when the other customers had left will be :

Pr(A > B + C) = 0

(2) when the service time are (i) with probability(pr) 1/3, i=1,2,3?

when service time i are (1,2,3) with probability
`(1)/(3)`

Then the event that A will be the last customer to complete service when the other two customers had left will occur when A = 3, B= 1, C= 1

Thus, the probability that A is the last customer to complete service when the other customers had left will be :

Pr ( A > B + C ) = Pr( A = 3, B = 1, C = 1)

Pr ( A > B + C ) =
`\begin {pmatrix} (1)/(3) \end {pmatrix}^3` given that the service times are independent

Pr ( A > B + C ) =
`\begin {pmatrix} (1)/(3) * (1)/(3) * (1)/(3) \end {pmatrix}`

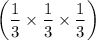
Pr ( A > B + C ) =
`\mathbf{(1)/(27)}`