Answer:
The first three terms of the original sequence are 9, 14, and 22.
Explanation:
From the question,
The first difference of the sequence is 5, 8, 11, 14,... That is,
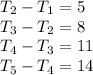
Where
 is the first term of the original sequence
is the first term of the original sequence
 is the second term of the original sequence
is the second term of the original sequence
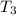 is the third term of the original sequence etc.
is the third term of the original sequence etc.
Also, from the question, the sum of the first two terms of the original sequence is 23; that is,

Now, we can find
 and
and
 by solving the following equations simultaneously
by solving the following equations simultaneously
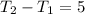 .......... (1)
.......... (1)
 ......... (2)
......... (2)
From equation (1)
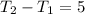
Then,
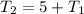 .......... (3)
.......... (3)
Substitute the value of
 into equation (2)
into equation (2)
Then,
 becomes
becomes
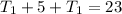
Then,

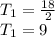
Hence, the first term of the original sequence is 9
Now, substitute the value of
 into equation (3)
into equation (3)
Then,
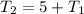 become
become
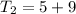
∴
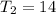
Hence, the second term of the original sequence is 14
The third term of the original sequence is given by
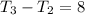
Then,
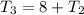
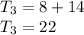
Hence, the third term of the original sequence is 22.
Hence, the first three terms of the original sequence are 9, 14, and 22.