Question

Tickets to the movies are $7 for adults and $4 for children. If 272 tickets

sold $1694, then how many of each type were sold?

Answer 1

202 tickets for adults were sold and 70 tickets for children are sold.

Explanation:

Solve this question using simultaneous linear equation.

•Let the number of tickets sold for adults be a

•Let the number of tickets sold for children be b

The question stated that 272 tickets were sold altogether. So:

`a + b = 272`

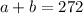
Now, make sure that only one of the unknown values remain on the left hand side. For example:

`a = 272 - b`

I will refer to the above equation as equation 1.

Now, the question also stated that the tickets sold $1694. This means that:

`7a + 4b = 1694`

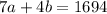
I will refer to this equation as equation 2.

Now, substitute equation 1 into equation 2 by replacing the a in equation 2 with the values on the right hand side in equation 1. For example:

`7(272 - b) + 4b = 1694`

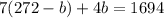
Then just solve the equation by finding the value of b.

`7(272 - b) + 4b = 1694 \\ 1904 - 7b + 4b = 1694 \\ 1904 - 3b = 1694 \\ 1904 - 1694 = 3b \\ 210 = 3b \\ b = 210 / 3 \\ = 70`

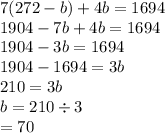
Lastly, find the value of a. Just take the value of b and then substitute into equation 1.

`a = 272 - b \\ = 272 - 70 \\ a = 202`