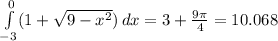Question

Evaluate the integral by interpreting it in terms of areas. integral -3 to 0(1+(9-x^2)^1/2)dx

Answer 1

`\int\limits^0_(-3)(1+\sqrt{9-x^(2)})\, dx=3+(9\pi)/(4)=10.068`

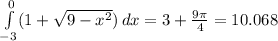
Explanation:

We need to evaluate the following integral by interpreting it in terms of areas :

`\int\limits^0_(-3)(1+\sqrt{9-x^(2)})\, dx`

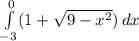
The first step is to separate the integral into two easier integrals

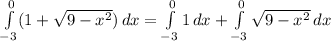`\int\limits^0_(-3)(1+\sqrt{9-x^(2)})\, dx=\int\limits^0_(-3) 1 \, dx+\int\limits^0_(-3)\sqrt{9-x^(2)}\, dx` (Integral of the sum)

Now we can calculate each integral by studying the area below each function.

For the first integral the function is
`f(x)=1`

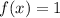
(I will attach a file with the functions)

The area below this function is the area of a rectangle with sides 1 and 3 ⇒

`\int\limits^0_(-3)1 \, dx=3`

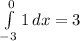
For the second integral the function is

`f(x)=y=\sqrt{9-x^(2)}`

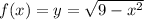
If we study this function :

`y=\sqrt{9-x^(2)}`

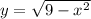
`y^(2)=9-x^(2)` (I)

`x^(2)+y^(2)=9`

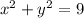
Which is the equation of a circle centered at (0,0) with radius equal to 3

From the equation (I)

`y^(2)=9-x^(2)`

`|y|=\sqrt{9-x^(2) }`

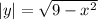
The two possible solutions are :

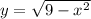`y=\sqrt{9-x^(2)}` (II) and
`y=-\sqrt{9-x^(2)}`

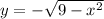
We will use (II) to solve the integral (which is the upper part of the circle)

The area of a circle with radius equal to 3 is

`\pi.3^(2)`

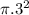
In the integral we only need a quarter of circle ⇒ We divide the total area by 4 ⇒
`(\pi.3^(2))/(4)` ⇒
`(9\pi )/(4)`

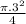Finally the integral is equal to

`\int\limits^0_(-3)(1+\sqrt{9-x^(2)})\, dx=3+(9\pi)/(4)=10.068`