Given :
A building is of unknown height. At a distance of 400 feet away from the building .
An observer notices that the angle of elevation to the top of the building is 35º and that the angle of elevation to a poster on the side of the building is 15º .
To Find :
How far is the poster from the roof of the building .
Solution :
Height is given by :
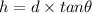
( Here ,
 is angle of elevation )
is angle of elevation )
So , height of tower :
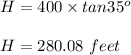
For height of poster :

Therefore , distance of poster from the roof of the building is :
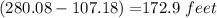
Hence , this is the required solution .